The ThomX Facility
Performances of Free Electron Laser (FEL) facilities (4th generation synchrotron facilities) are in constant rise. But their exploitation needs more ressources.
Various applications, like chemical analysis (Cotte, et al., 2007), medical (Suortti & Thomlinson, 2003) (Ando, et al., 2005), cristallography (Mc Gee, 2007), radioactive waste management (Hajima, Hayakama, Kikuzawa, & Minehara, 2008) or museology (De Viguerie, Walter, Laval, Mottin, & Armando Solé, 2010) uses X-rays with flux level situated between FEL and rotating anode X-rays generators (Figure 2‑1 (Variola, Loulergue, & Zomer, 2010)). X-rays produced by Inverse Compton Backscattering are an interesting alternative regarding their performances, their compacity and the use of standards parts.
ThomX will demonstrate that a very compact accelerators could produced high flux and high energy X-rays using Inverse Compton Backscattering effect.
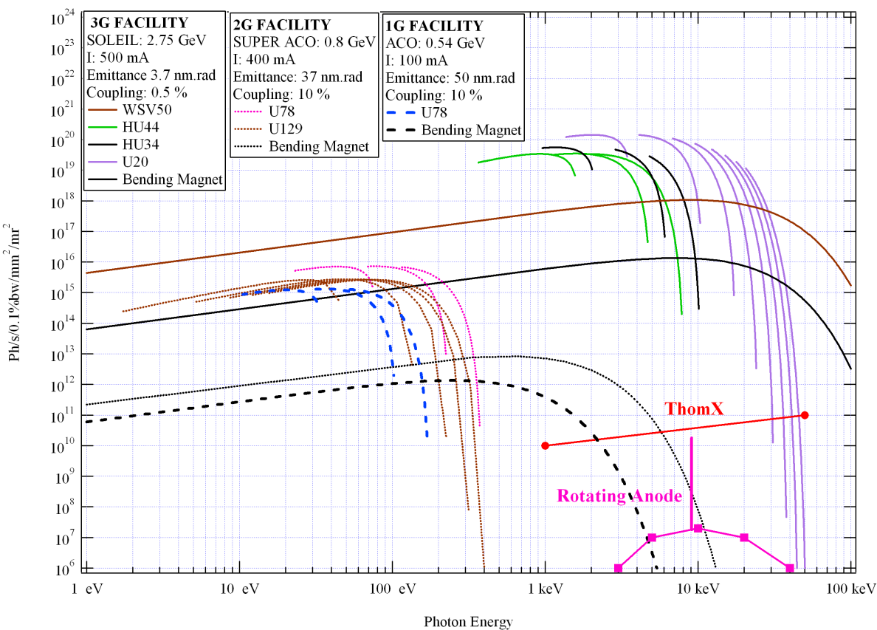
Photon flux versus energy for various synchrotron sources compared to the performances of rotating anode generators and ThomX. Energy and flux ranges cover by ThomX are intermediate with the synchrotron facilities (Super ACO, SOLEIL) and rotating anode generators. (Variola, Loulergue, & Zomer, 2010).
The table below described the main parameters from the sub-systems of the ThomX facility
| Parameters | Value |
| LINAC (gun and accelerating cavity) | |
| Charge | 1 nC |
| Wavelength of the photocathode laser | 257 nm |
| Normalized emittance rms | 4,4π mm.mrad |
| Energy spread | 0,4% |
| Storage Ring | |
| Energy | 70 MeV |
| Collision angle at the IP | 2° |
| Bunch length (at injection) | 4 ps |
| Bunch length after 20ms of storage | 50 ps |
| Current | 17,8 mA |
| Fabry-Perot Cavity | |
| Laser Wavelength | 1030 nm |
| Laser power | 50-100 W |
| Energy of the laser pulse | 1,4 – 2,8 µJ |
| Energy of the laser pulse in the Fabry-Perot cavity | 28 mJ |
| Pulse wavelength in the Fabry-Perot cavity | 5 ps |
| Fabry-Perot finesse | 3000-30000 |
| Power in the Fabry-Perot cavity | 0,07 – 0,7 MW |
| X-rays produced by Invers Compton backsterring effect | |
| Maximum energy | 90 keV |
| Total Flux | 1011-1013 photons.s-1 |
Inverse Compton Backscattering Effect
The Thomson Effect is the scattering of an electromagnetic wave (photon), with the frequency ωγ ,on an electron with the mass at rest equal to me (elastic scattering). The differential cross-section for the Thomson scattering could be written as (Compton, The spectrum of scattered X-rays, 1923) (Compton, A quantum theory of the scaterring of X-rays by light elements, 1923) :
Differential cross-section for Thomson scattering
Where:
- σTh : cross-section for Thomson scattering;
- r0 ~ 2.8.10-15 m : electron radius;
- Ω : solid angle of the photon scattering;
- θ : angle of the photon scattering regarding the initial direction.
If integrate in every angles, classic cross-section (non-relativistic electron) for the Thomson scattering is: σTh = 0.67 barn.
In the current case, electron recoil is neglected. If recoil is not neglected, photon give a fraction of it energy to the electron. The frequency of the photon is then modified, from ωi to ωf. The cross-section of the Compton scattering could be calculated with the formula of Klein-Nishina (Klein & Nishina, 1929):
Formula of Klein-Nishina to calculate the cross section the Compton scattering with an electron at rest
Where:
- α : thin structure constant;
 : Compton electron wavelength with me : electorn mass at rest ;
: Compton electron wavelength with me : electorn mass at rest ;- Eγ : initial energy of the photon;
 .
.
For non-polarized electrons and photons, the differential cross-section of Compton scattering in the laboratory frame can be written as:
Differential cross-section of Compton scattering in the laboratory frame
If the electrons move with a moment pe, a part of the energy is transferred to the incident photon. In the laboratory frame, the photon is backscattered with more energy: this is the Inverse Compton backscattering effect (Endo, 2012)).
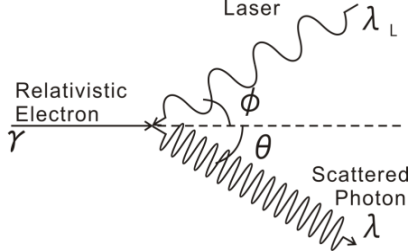
Inverse Compton backscattering effect. A relativistic electron (Lorentz factor >>1) collides with a photon with a wavalegth equal to λL and with an angle of Φ. A fraction of the electron energy is transferred to the photon which is backscatterd with an angle θ and an energy λ>λL
With ultra-relativistic electrons[1], their polarization acts on the energy spectrum of the photons produced. la polarisation des électrons aura un effet sur le spectre en énergie des photons issus de la rétrodiffusion. The differential cross-section of the Compton backscattering (Barber, et al., 1993) for relativistic electrons is a function of the polarization vector of the electron P(Px, Py, Pz) and the Stokes polarization(Born & Wolf, 1959) of the photons S(S0, S1, S2, S3):
Differential cross-section of the Compton backscattering for relativistic electron with electron and photon polarization
Where:
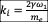 ;
; ;
;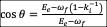 ;
;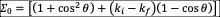 ;
; ;
; ;
;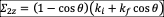 .
.
The Klein-Nishina formula can be retrieved if there is no polarization. The polarization of the photons changes the spectra of the backscattered photons as a function of the energy of the incident electrons. Nevertheless, it is negligeable in the energy range of ThomX
Energy gain for backscatterd photons on ultra-relativistic electrons can be described with the formula above, in the laboratory frame (with the parameters given in the following illustration):
Frequency gain of the backscattered photons produced by the Inverse Compton backscattering on ultra-relativistic photons
As γ>>1, the previous formula can be written as:
Frequency gain of the backscattered photons produced by the Inverse Compton backscattering on ultra-relativistic photons, limited development for γ>>1
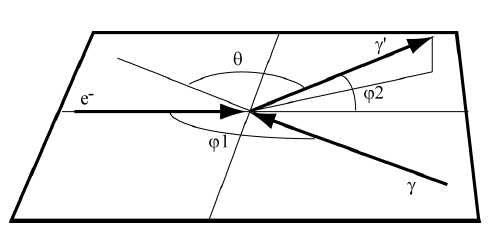
Inverse Compton backscattering effect between an electron and a photon with a wavelength γ and angle φ1. Photons are backscattered with an angle φ2 and with a wavelength γ’>γ (Variola, Haissinski, Loulergue, & Zomer, 2013).
These specific characteristics can be described regarding the previous formula:
- The wavelength of the backscattered photons vary with the backscattered angle. Thus, specific wavelength can be choosen regarding the angular divergence;
- The emmited cone of the backscattered photon is weak, the total angular divergence is around 4/γ;
- The maximum energy of the backscattered photon is obtained with a head-on collision, ϕ1=π:
 .
.
The luminosity created by the collision between two gaussian beams can be described with the following formula (Suzuki T. , 1976):
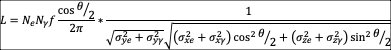
Luminosity created by the collision of two gaussian beams
Where:
- Ne: number of electron by bunch;
- Nγ: number of photons by bunch;
- f: collision repetition rate;
- σ(x, y, z)e, σ(x, y, z)γ : 3-D size of the electrons and photons bunches.
The production rate of photons is equal to:
Production rate of photons
The photon flux is a function of the electrons charge, the initial photon flux and the collision repetition rate. It could be noted that a little variation of the collision angle can modify largely the flux (see picture above). For ThomX, the collision angle is equal to 2 degrees.
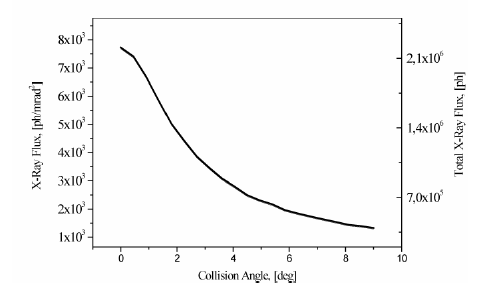
Variation the the X-rays flux with the collision angle (Bruni, et al., 2010)
The accelerator
The ThomX facility will produce ultra-relativistic electrons and photons with high repetition rate and large flux in order to create the most interesting X-rays beam for the scientific research. At this purpose, the machine is made with these mains parts:
- a linear accelerator with a photocathode gun and a accelerating section
- a transfer line from the LINAC to the storage ring
- a storage ring
- a laser source amplified with a Favbry-Perot interferometer
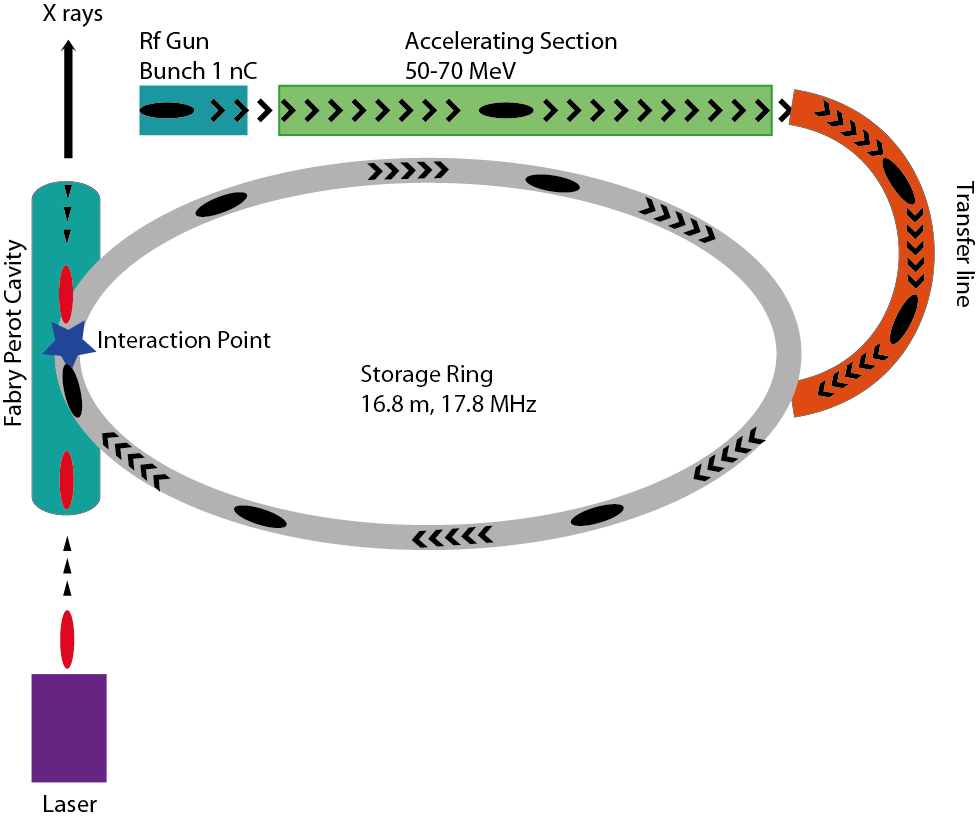
Schematic layout of the ThomX facility. Electrons creatd by the RF gun are accelerated through the accelerating section. The transfer line fills the storage ring with the accelerated electrons. The electrons bunches collide with a amplified laser (with a Fabry-Perot cavity) to produce X-rays using the Inverse Compton Backscattering effect. (Variola, Haissinski, Loulergue, & Zomer, 2013)
The RF gun will produce electrons beam with a charge up to 1,5 nC, an emittance inferior to 5 mm.mrad and an energy spread inferior to 1%. The repetition rate will be equal to 50 Hz and the buch length equal to 5 ps.
The storage ring must keep optimal charateristics for the electron beam at the interaction point. The size, the energy spread and the bunch length must be equal to the initial value. The size of the various parts is limited too by the aim of compacity.
The design layout is presented in the picture above. The optic line (8 dipoles, 24 quadripoles and 12 sextupoles) keeps the optimal beam characteristics and a RF cavity is used to compensate the energy losses during the storage.
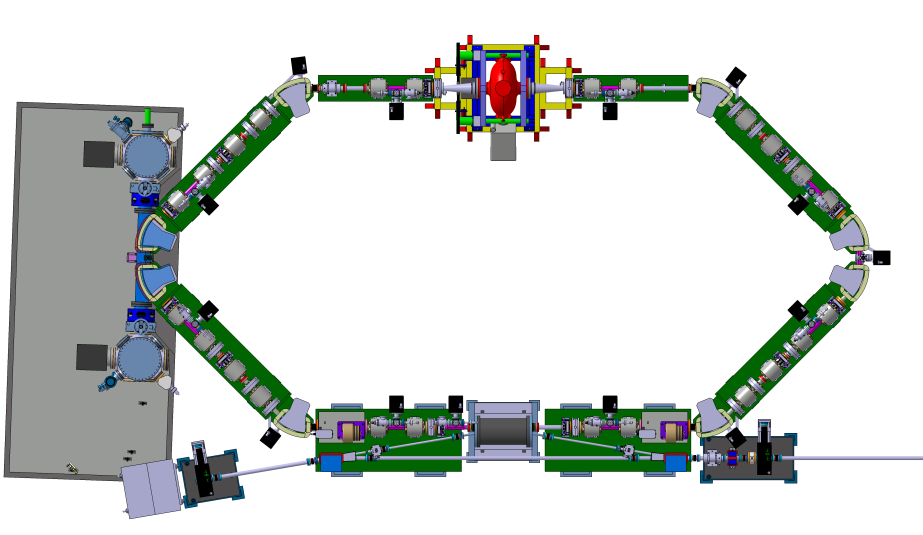
Design layout of the ThomX storage ring (Variola, Haissinski, Loulergue, & Zomer, 2013)
The electron bunch in the storage ring is renewed 50 times per second using a septum/kicker system (see picture above).
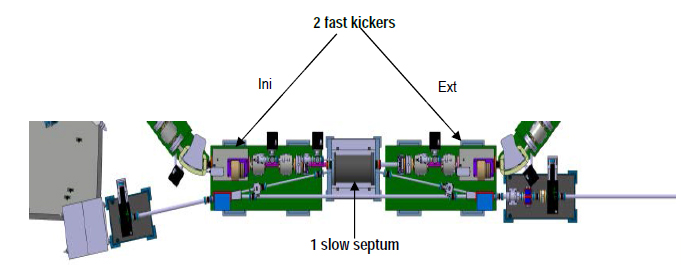
Septum/kicker system integrated in the ThomX storage ring (Variola, Haissinski, Loulergue, & Zomer, 2013)
X-rays luminosity is proportional to the number of photons and the collision repetition rate. Regarding the cross-section (for ThomX, σICS~0,7 barns), the X-rays production rate is increased by a high flux of photons. To reach the required performances for the laser photons (a power equal to 0,7 MW and a repetition rate of 40 MHz at the IP), an Fabry-Perot cavity is used. The principle is to use the resonance of a planar wave on itself to amplify the initial photon beam (produced by a laser with a mean power equal to 100 W). At this purpose, the laser is reflected by mirrors separated by a distance L proportionnal to the wavelength of the photons λ. The resonance could be reached following this formula:
Condition to reach the resonance in a Fabry-Perot Cavity
Where:
- q is positive integer;
-
 : Laser repetition rate.
: Laser repetition rate.
The cavity developped for ThomX facility, made with four mirrors, can reach high finesse values, up to 30 000.
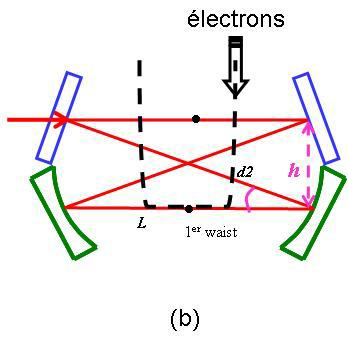
Design layout of a four-mirrors Fabry-Perot cavity (Variola, Loulergue, & Zomer, 2010).
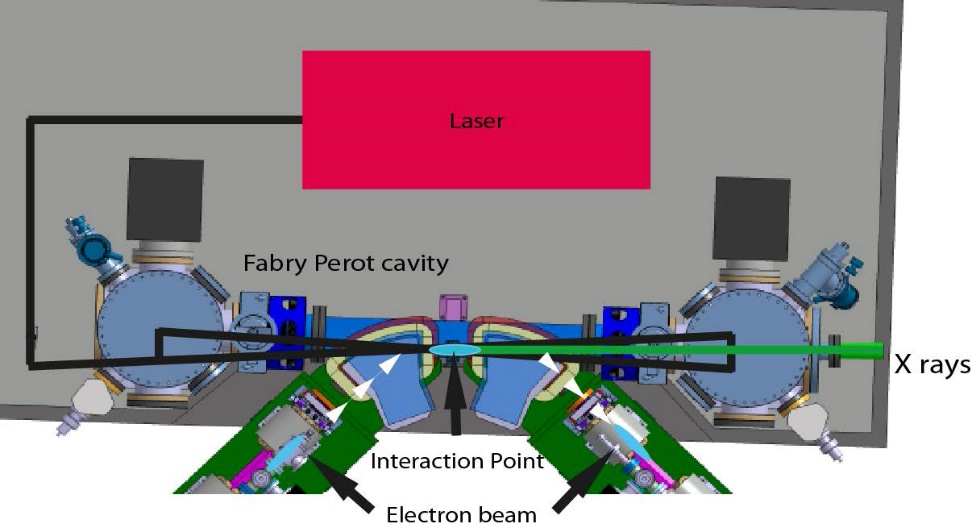
Integration of the Fabry-Perot cavity into the storage ring (Variola, Haissinski, Loulergue, & Zomer, 2013).
[1] An relativistic electron has a kinetic energy superior to the electron mass at rest (0,511 MeV). An electron is ultra-relativistic when the Lorentz factor γ is widely superior to 1
[2] The finesse of a resonator is defined as the number of going and coming made in the cavity befor the beam goes out.
